Codility - Lesson 6 Sorting - 4. NumberOfDiscIntersections (simple solution)

Source Link:
https://codility.com/programmers/lessons/6-sorting/number_of_disc_intersections/

Question:

We draw N discs on a plane. The discs are numbered from 0 to N − 1. A zero-indexed array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].
We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).
The figure below shows discs drawn for N = 6 and A as follows:
A[0] = 1 A[1] = 5 A[2] = 2 A[3] = 1 A[4] = 4
A[5] = 0
 
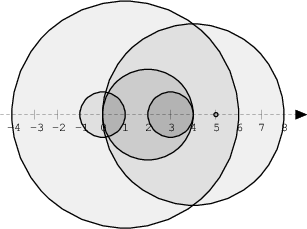
There are eleven (unordered) pairs of discs that intersect, namely:

• discs 1 and 4 intersect, and both intersect with all the other discs;
• disc 2 also intersects with discs 0 and 3.

Write a function:

class Solution { public int solution(int[] A); }

that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.
Given array A shown above, the function should return 11, as explained above.
Assume that:

• N is an integer within the range [0..100,000];
• each element of array A is an integer within the range [0..2,147,483,647].

Complexity:

• expected worst-case time complexity is O(N*log(N));
• expected worst-case space complexity is O(N), beyond input storage (not counting the storage required for input arguments).

Elements of input arrays can be modified.

My Solution:
Notes:
1. This is a simple solution with O(n^2) the performance score is low (but 100% correct)
2. main idea:
// 1. store all the "lower points" and "upper points" of the discs
// 2. count the intersections (if one upper point "is bigger than or equal to" one lower point)  
3. use "long" for big numbers (be careful)
long[] lower = new long[A.length];
long[] upper = new long[A.length];
for(int i=0; i<A.length; i++){
lower[i] = i - (long)A[i]; // note: lower = center - A[i]
upper[i] = i + (long)A[i]; // note: upper = center + A[i]
}  
4. scan the upper points
for(int i=0; i<A.length; i++){
// note: compare "i" with "j": need to set "j=i+1" (avoid double counting)
for(int j = i+1; j<A.length; j++){
// intersection: when one's upper is bigger than "or equal to" one's lower (important)
if(upper[i]>=lower[j]){ // note: when "equal to", there is also an intersection
intersection++;
}
}
}   
5. for the overflow cases
if(intersection > 10_000_000)
return -1;